User:Zelenka/Statistics/exercises 23.10.2007
From eqqon
23.10.2007
- 17) Um die Dauer einer Meisterschaft abzukürzen, werden die 2n teilnehmenden Teams durch Los in zwei gleich große Untergruppen aufgeteilt. Mit welcher Wahrscheinlichkeit sind dann die zwei stärksten Teams in derselben Gruppe? Ermitteln Sie einen möglichst einfachen Ausdruck.
- 18) Vier symmetrische Würfel werden geworfen
- (a) Mit welcher Wahrscheinlichkeit ist die Augensumme gleich 18 ?
- (b) Angenommen, einer der vier Würfel zeigt 5. Mit welcherWahrscheinlichkeit ist dann die Augensumme gleich 18 ?
wVkn = 64 = 1296 Variationen
int i,j,k,l,sum=0;
for(i=1;i<=6;i++)
{
for(j=1;j<=6;j++)
{
for(k=1;k<=6;k++)
{
for(l=1;l<=6;l++)
{
if((i+j+k+l == 18) && (i==5 || j==5 || k==5 || l==5))
{
sum++;
Console.WriteLine("{0} {1} {2} {3}",i,j,k,l);
}
}
}
}
}
Console.WriteLine("sum:{0}",sum);
Summe=18 Summe=18 und ein Würfel zeigt 5 1 5 6 6 1 5 6 6 1 6 5 6 1 6 5 6 1 6 6 5 1 6 6 5 2 4 6 6 2 5 5 6 2 5 5 6 2 5 6 5 2 5 6 5 2 6 5 5 2 6 4 6 3 4 5 6 2 6 5 5 3 4 6 5 2 6 6 4 3 5 4 6 3 3 6 6 3 5 5 5 3 4 5 6 3 5 6 4 3 4 6 5 3 6 4 5 3 5 4 6 3 6 5 4 3 5 5 5 4 3 5 6 3 5 6 4 4 3 6 5 3 6 3 6 4 4 5 5 3 6 4 5 4 5 3 6 3 6 5 4 4 5 4 5 3 6 6 3 4 5 5 4 4 2 6 6 4 5 6 3 4 3 5 6 4 6 3 5 4 3 6 5 4 6 5 3 4 4 4 6 5 1 6 6 4 4 5 5 5 2 5 6 4 4 6 4 5 2 6 5 4 5 3 6 5 3 4 6 4 5 4 5 5 3 5 5 4 5 5 4 5 3 6 4 4 5 6 3 5 4 3 6 4 6 2 6 5 4 4 5 4 6 3 5 5 4 5 4 4 6 4 4 5 4 6 3 4 6 5 3 5 5 2 6 4 6 6 2 5 5 3 5 5 1 6 6 5 5 4 4 5 2 5 6 5 5 5 3 5 2 6 5 5 5 6 2 5 3 4 6 5 6 1 6 5 3 5 5 5 6 2 5 5 3 6 4 5 6 3 4 5 4 3 6 5 6 4 3 5 4 4 5 5 6 5 2 5 4 5 4 5 6 6 1 5 4 6 3 6 1 5 6 5 5 2 6 6 1 6 5 5 5 3 5 6 2 5 5 5 5 4 4 6 3 4 5 5 5 5 3 6 3 5 4 5 5 6 2 6 4 3 5 5 6 1 6 6 4 5 3 5 6 2 5 6 5 1 6 5 6 3 4 6 5 2 5 5 6 4 3 6 5 3 4 5 6 5 2 6 5 4 3 5 6 6 1 6 5 5 2 6 1 5 6 6 5 6 1 6 1 6 5 6 6 1 5 6 2 4 6 6 6 5 1 6 2 5 5 sum:58 6 2 6 4 6 3 3 6 6 3 4 5 6 3 5 4 6 3 6 3 6 4 2 6 6 4 3 5 6 4 4 4 6 4 5 3 6 4 6 2 6 5 1 6 6 5 2 5 6 5 3 4 6 5 4 3 6 5 5 2 6 5 6 1 6 6 1 5 6 6 2 4 6 6 3 3 6 6 4 2 6 6 5 1 sum:80
Lösung:
- p(sum 18) = 80/1296 = 0,0617
- p(sum 18 und 1 Würfel zeigt 5) = 58/1296 = 0,045
- 20. Zwei Wanderer erreichen aus unterschiedlichen Richtungen einen Aussichtspunkt und halten sich dort 10 Minuten (Wanderer 1) bzw. 20 Minuten (Wanderer 2) auf. Ihre Ankunftszeitpunkte liegen – unabhängig voneinander – zufällig zwischen 11 und 12 Uhr.
- (a) Mit welcher Wahrscheinlichkeit begegnen sie einander am Aussichtspunkt?
- (b) Wie groß ist unter den gegebenen Bedingungen die Wahrscheinlichkeit, daß sich um 11:30 (1) keiner, (2) genau einer, (3) beide am Aussichtspunkt befinden?
- 22) Jemand verläßt zufällig zwischen 15 und 17 Uhr seinen/ihren Arbeitsplatz und begibt sich zur U–Bahn. Seine/Ihre Mutter lebt in der Nähe der einen Endstation, seine/ihr Freundin/Freund in der Nähe der anderen. Er/Sie will fair sein und nimmt jeweils diejenige U–Bahn, welche als erste eintrifft. Nach einiger
Zeit beklagt sich die Mutter darüber, daß er/sie nur ganz selten zum Abendessen kommt, an den letzten 20 Arbeitstagen nur zweimal. Kommt dieses Ungleichgewicht zufällig zustande oder gibt es eine andere Erklärung dafür?
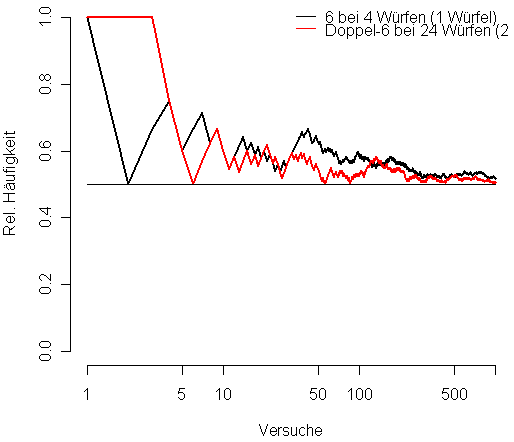
- 23) Der französische Offizier und Schriftsteller Chevalier de Méré (1607 – 1684) wandte sich im Jahre 1654 mit der folgenden Frage an Blaise Pascal (1623 – 1662): Was ist vorteilhafter, beim Spiel mit einem Würfel auf das Eintreten mindestes eines Sechsers in vier Würfen oder beim Spiel mit zwei Würfeln auf das Eintreten eines Doppelsechsers in 24 Würfen zu setzen? Er wußte aus Erfahrung, daß die erste Wette für ihn vorteilhaft ist; bei der zweiten Wette, von der er annahm, daß sie nur eine Variante der ersten sei, gestalteten sich die Einnahmen aber nicht nach seinen Vorstellungen.
- (a) Bearbeiten Sie das Problem zunächst empirisch (Empirisches Gesetz der Großen Zahlen). Nehmen Sie dazu (z.B.) das folgende R–Script:
versuche <- 1000
n <- versuche*4
x <- matrix(sample(1:6, n, replace=TRUE), nrow=versuche, ncol=4)
sechs.in.4 <- apply(x==6, 1, any)
freq.6.in.4 <- cumsum(sechs.in.4)/(1:versuche)
n <- versuche*48
x <- matrix(sample(1:6, n, TRUE), nrow=versuche, ncol=48)
doppel.6.in.24 <- apply(x==6, 1, function(x) any(x[1:24] & x[25:48]))
freq.doppel.6.in.24 <- cumsum(doppel.6.in.24)/(1:versuche)
plot(freq.6.in.4, ylim=0:1, log="x", type="l", bty="n", lwd=2,
ylab="Rel. Häufigkeit", xlab="Versuche")
lines(1:versuche, freq.doppel.6.in.24, lty=1, lwd=2, col=2)
lines(c(1,versuche), c(0.5,0.5), lty=1)
legend("topright", legend=c("6 bei 4 Würfen (1 Würfel)",
"Doppel-6 bei 24 Würfen (2 Würfel)"), bty="n", lty=1, col=1:2)
- (b) Wie lautet die exakte Lösung?
- 24)
- (a) Für jedes (eindimensionale) Ereignis A sei eine Wahrscheinlichkeit wie folgt definiert:
- W(A) =Σ f(x) mit f(x) = (2/3)*(1/3)x , x = 0, 1, 2, . . . (f(x) = 0 sonst)
- Wenn A1 = {x : x = 0, 1, 2, 3} und A2 = {x : x = 0, 1, 2, . . .}, bestimmen Sie W(A1) und W(A2).
- (b) Für jedes (eindimensionale) Ereignis A sei eine Wahrscheinlichkeit wie folgt definiert:
- W(A) = ∫ f(x) dx mit f(x) = 6x(1 − x) I(0,1)(x) (Existiert das Integral nicht, ist W(A) nicht definiert.)
- Wenn A1 = {x : 1/4 < x < 3/4 }, A2 = { 1/2 } und A3 = {x : 0 < x < 10}, bestimmen Sie W(A1), W(A2) und W(A3).