User:Zelenka/Statistics/exercises 9.10.2007

From eqqon

9.10.2007

2. R-script

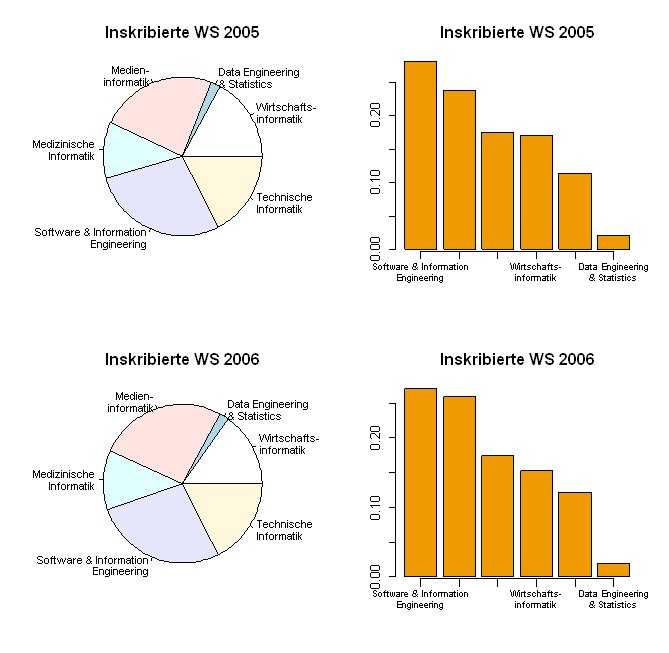
Im WS 2005 und 2006 verteilten sich die Inskriptionszahlen der Studienrichtungen, für die die VO/UE Statistik u. Wahrscheinlichkeitstheorie anrechenbar bzw. verpflichtend ist, wie unten angegeben (Quelle: TUWIEN). Erstellen Sie vergleichende Balken– und Kreisdiagramme für die Gesamtzahlen (oder für Teilzahlen). Gibt es „signifikante“ Veränderungen?

Zahlen für WS 2005

	Inländer		Ausländer
KNR Studienrichtung	Forts.	Anf.	Forts.	Anf.	Summe
526 Wirtschaftsinformatik	497	106	142	24	769
531 Data Egineering & Statistics	55	14	22	3	94
532 Medieninformatik	645	210	180	33	1068
533 Medizinische Informatik	285	104	101	24	514
534 Software & Information Engineering	702	167	336	61	1266
535 Technische Informatik	427	117	205	37	786

Zahlen für WS 2006

	Inländer		Ausländer
KNR Studienrichtung	Forts.	Anf.	Forts.	Anf.	Summe
526 Wirtschaftsinformatik	459	132	126	19	736
531 Data Egineering & Statistics	55	11	22	4	92
532 Medieninformatik	770	226	223	34	1253
533 Medizinische Informatik	368	80	118	17	583
534 Software & Information Engineering	771	146	352	39	1308
535 Technische Informatik	484	94	229	38	845

Nehmen Sie (z.B.) das folgende R–Script. Informieren Sie sich über die dabei verwendeten Funktionen und deren Argumente (help(name)). R-Script:

x2005 <- c(769,94,1068,514,1266,786)
x2006 <- c(736,92,1253,583,1308,845)
Studien <- c("Wirtschafts-\ninformatik","Data Engineering\n& Statistics",
"Medien-\ninformatik","Medizinische\nInformatik",
"Software & Information\nEngineering","Technische\nInformatik")
names(x2005) <- names(x2006) <- Studien
par(mfrow=c(2,2))
pie(x2005, radius=0.9, main="Inskribierte WS 2005", cex=0.8)
barplot(sort(x2005, decreasing=TRUE)/sum(x2005), axis.lty=1, cex.names=0.7,
col="orange2", main="Inskribierte WS 2005")
pie(x2006, radius=0.9, main="Inskribierte WS 2006", cex=0.8)
barplot(sort(x2006, decreasing=TRUE)/sum(x2006), axis.lty=1, cex.names=0.7,
col="orange2", main="Inskribierte WS 2006")
par(mfrow=c(1,1))

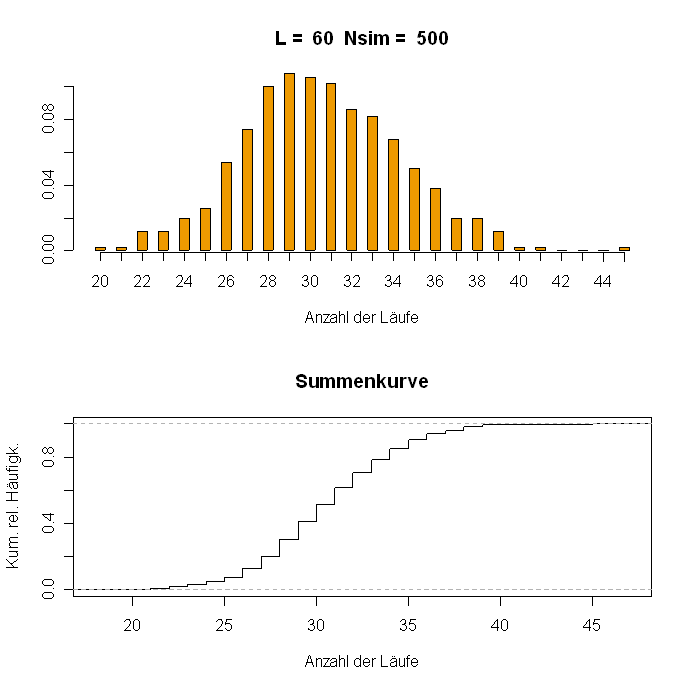
3. Ist x1, . . . , xL eine Binärfolge der Länge L, so heißt die Teilfolge xi+1, . . . , xi+k ein Lauf (engl. run) der

Länge k, falls:

(1) i = 0 oder xi 6= xi+1

(2) xi+1 = · · · = xi+k

(3) i + k = L oder xi+k 6= xi+k+1

Ist beispielsweise L = 10 und lautet die Binärfolge:

0 0 1 0 0 0 1 1 0 0

so gibt es 5 Läufe mit den Längen 2, 1, 3, 2, 2.

Das folgende R–Script bestimmt die Zahl der Läufe von N simulierten Binärfolgen (mit gleicher Wahrscheinlichkeit für 0 und 1) der Länge L, ermittelt eine Häufigkeitstabelle und stellt das Ergebnis in Form eines Stabdiagramms und einer Summenkurve dar. Experimentieren Sie mit verschiedenen Werten für N und L und kommentieren Sie die Ergebnisse. R–Script:

#Bestimmung der Zahl der Läufe für Binärfolge x
RunNumber <- function(x) {
n <- length(x)
z <- x
z[n+1] <- ifelse(x[n]==0, 1, 0)
y <- abs(diff(z))
Index1 <- c(1:n)
Index <- c(0,Index1[y==1])
Number <- length(diff(Index))
return(Number) }

#Simulation
N <- 500
L <- 60
x <- matrix(rbinom(N*L, 1, 1/2), nrow=N)
NumberRuns <- apply(x, 1, RunNumber)

#Häufigkeitstabelle
tab1 <- table(NumberRuns)
mr <- as.numeric(names(tab1))
n1 <- min(mr)
n2 <- max(mr)
nk <- numeric(n2-n1+1)
nk[mr-n1+1] <- tab1
names(nk) <- n1:n2
par(mfrow=c(2,1))

#Stabdiagramm
barplot(nk/N, axis.lty=1, space=1, xlab="Anzahl der Läufe",
main=paste("L = ", L, " Nsim = ", N), col="orange2")

#Summenkurve
plot(ecdf(NumberRuns), verticals=TRUE, do.points=FALSE,
xlab="Anzahl der Läufe", ylab="Kum. rel. Häufigk.",
main="Summenkurve")
par(mfrow=c(1,1))

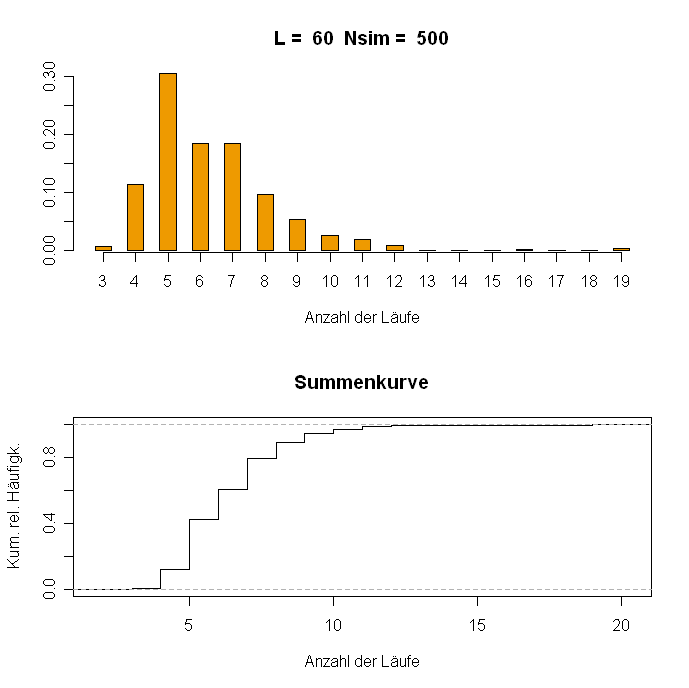
4. [Fortsetzung von Aufgabe 3] Neben der Anzahl der Läufe ist auch die Länge des längsten Laufs von Interesse. Modifizieren Sie das obige Script so, daß zu jeder simulierten Binärfolge die Länge des längsten Laufs bestimmt, die entsprechende Häufigkeitstabelle ermittelt und das Ergebnis in Form eines Stabdiagramms und einer Summenkurve dargestellt wird.

Hinweis: Nur ganz wenige Änderungen sind erforderlich. In der Funktion muß nur eine Zeile verändert werden (max statt length in der vorletzten Zeile). Der Rest kann nahezu unverändert übernommen werden.

#Bestimmung der Zahl der Läufe für Binärfolge x
RunNumber <- function(x) {
n <- length(x)
z <- x
z[n+1] <- ifelse(x[n]==0, 1, 0)
y <- abs(diff(z))
Index1 <- c(1:n)
Index <- c(0,Index1[y==1])
Number <- max(diff(Index))
return(Number) }

#Simulation
N <- 500
L <- 60
x <- matrix(rbinom(N*L, 1, 1/2), nrow=N)
NumberRuns <- apply(x, 1, RunNumber)

#Häufigkeitstabelle
tab1 <- table(NumberRuns)
mr <- as.numeric(names(tab1))
n1 <- min(mr)
n2 <- max(mr)
nk <- numeric(n2-n1+1)
nk[mr-n1+1] <- tab1
names(nk) <- n1:n2
par(mfrow=c(2,1))

#Stabdiagramm
barplot(nk/N, axis.lty=1, space=1, xlab="Anzahl der Läufe",
main=paste("L = ", L, " Nsim = ", N), col="orange2")

#Summenkurve
plot(ecdf(NumberRuns), verticals=TRUE, do.points=FALSE,
xlab="Anzahl der Läufe", ylab="Kum. rel. Häufigk.",
main="Summenkurve")
par(mfrow=c(1,1))

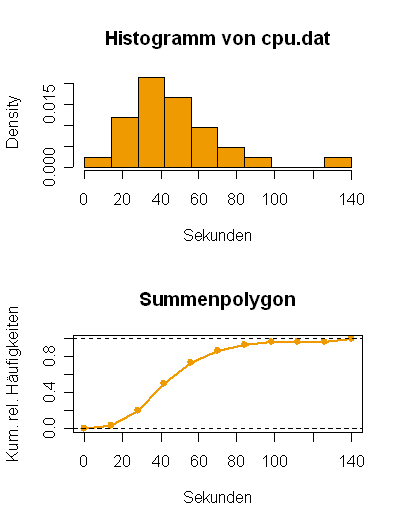
5. Um die Effizienz eines Prozessors für eine bestimmte Art von Aufgaben beurteilen zu können, wurden die

CPU–Zeiten (Sekunden) für n = 30 zufällig ausgewählte Jobs gemessen (cpu.dat):

70 36 43 69 82 48 34 62 35 15
59 139 46 37 42 30 55 56 36 82
38 89 54 25 35 24 22 9 56 19

(a) Ermitteln Sie eine Häufigkeitstabelle. Nehmen Sie dazu äquidistante Klassen der Breite 14 [Sekunden], beginnend bei 0. (b) Erstellen Sie auf Basis von (a) das Histogramm der relativen Klassenhäufigkeiten. (c) Zeichnen Sie auf Basis der gewählten Klasseneinteilung das Summenpolygon.

(d) Wie beurteilen Sie die größte Beobachtung 139 ?

Der Wert 139 ist ein "Ausreisser". Dieser Wert muss daher genauer untersucht werden, ob er durch einen Ablesefehler entstanden ist, die Versuchsbedingungen verändert waren oder tatsächlich so grosse Streuung möglich ist.

R–Script:

cpu <- read.table("cpu.dat", header=TRUE)
x <- cpu$x
n <- length(x)

#Histogramm
breaks <- seq(0,140,by=14)
m <- length(breaks)
x.hist <- hist(x, breaks=breaks, prob=TRUE, col="orange2",
xlab="Sekunden", main="Histogramm von cpu.dat")
(freq <- x.hist$counts)

#Summenpolygon
plot(breaks,c(0,cumsum(freq)/n), type="o", lty=1, pch=19, lwd=2,
col="orange2", xlab="Sekunden", ylab="Kum. rel. Häufigkeiten",
main="Summenpolygon")
abline(h=c(0,1), lty=2)

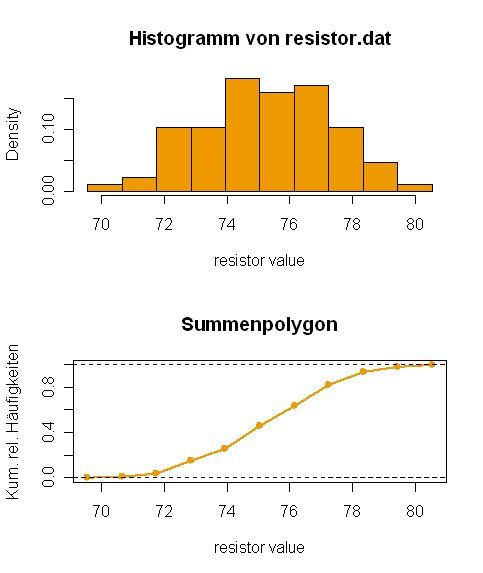
6. Der folgende Datensatz enthält Messungen (in Ohm) von 80 Widerständen (resistor.dat)

74.4 77.3 77.4 74.3 69.6 71.3 72.5 77.4 73.5 76.1
75.6 75.5 73.3 74.3 77.2 75.1 75.1 79.3 75.8 77.1
76.9 75.8 73.3 74.8 74.7 76.4 78.7 78.5 77.4 74.0
73.2 72.3 76.9 76.2 76.3 74.1 77.0 74.1 72.5 72.7
73.6 78.4 77.7 71.6 73.2 76.4 71.8 78.1 75.6 74.0
75.0 77.5 76.4 72.5 72.8 71.8 73.1 75.0 77.7 77.9
76.2 75.0 76.4 76.3 73.1 74.7 76.0 75.6 75.3 79.6
74.6 77.0 72.1 75.2 75.7 74.7 73.6 75.2 76.6 74.6

(a) Ermitteln und zeichnen Sie die empirische Verteilungsfunktion. Hinweis: Nehmen Sie die Funktion ecdf() (= empirical cumulative distribution function).

(b) Stellen Sie die Verteilung der relativen Klassenhäufigkeiten in Form eines Histogramms dar. Nehmen Sie dazu beispielsweise die folgende äquidistante Klasseneinteilung:

[69.55, 70.65], (70.65, 71.75], . . . , (79.45, 80.55] Wählen Sie die Darstellung so, daß die Fläche unter dem Histogramm gleich 1 ist (Dichtehistogramm oder flächentreues Histogramm genannt).

(c) Zeichnen Sie auf Basis der obigen Klasseneinteilung das Summenpolygon.

(d) Nehmen Sie andere Klasseneinteilungen und kommentieren Sie die Ergebnisse. Ändert sich der Eindruck hinsichtlich der Form der Verteilung?

Wenn man die Klasseneinteilung zu fein macht, werden die Balken unterbrochen, das Diagramm "ausgefranst".

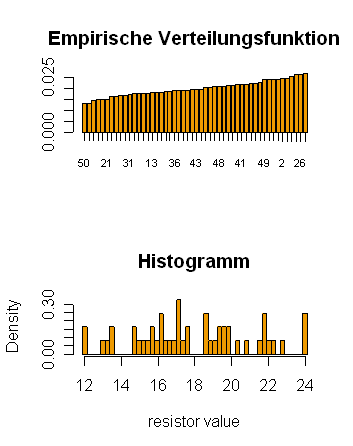
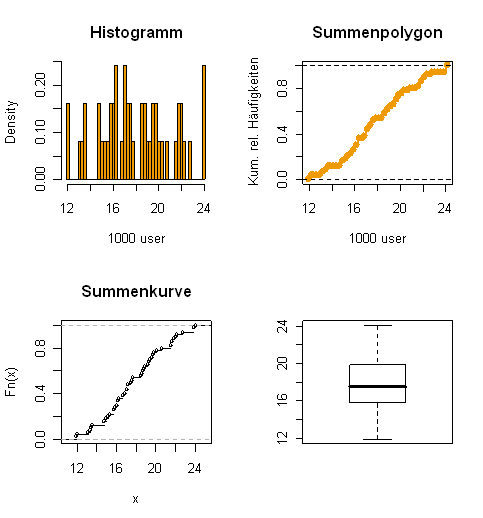
7. Ein Netzwerkprovider untersucht die Belastung seines Netzwerks. Dazu wird an 50 Stellen im Netz die

Anzahl (in 1000 Personen) der gleichzeitigen User bestimmt (concurrent.dat):

17.2 22.1 18.5 17.2 18.6 14.8 21.7 15.8 16.3 22.8
24.1 13.3 16.2 17.5 19.0 23.9 14.8 22.2 21.7 20.7
13.5 15.8 13.1 16.1 21.9 23.9 19.3 12.0 19.9 19.4
15.4 16.7 19.5 16.2 16.9 17.1 20.2 13.4 19.8 17.7
19.7 18.7 17.6 15.9 15.2 17.1 15.0 18.8 21.6 11.9

(a) Ermitteln und zeichnen Sie die empirische Verteilungsfunktion.

(b) Stellen Sie die Verteilung der relativen Klassenhäufigkeiten in Form eines Histogramms dar.

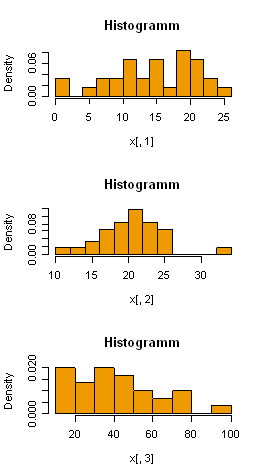
8. Betrachten Sie die folgenden drei Datensätze (threesets.dat)

(1) 19 24 12 19 18 24 8 5 9 20 13 11 1 12 11 10 22 21 7 16 15 15 26 16 1 13 21 21 20 19

(2) 17 24 21 22 26 22 19 21 23 11 19 14 23 25 26 15 17 26 21 18 19 21 24 18 16 20 21 20 23 33

(3) 56 52 13 34 33 18 44 41 48 75 24 19 35 27 46 62 71 24 66 94 40 18 15 39 53 23 41 78 15 35

(a) Zeichnen Sie zu jedem Datensatz ein Histogramm und bestimmen Sie, ob die Verteilung rechtsschief, linksschief oder (annähernd) symmetrisch ist.

(b) Berechnen Sie zu jedem Datensatz den Mittelwert und den Median. Unterstützen diese Werte die Ergebnisse von (a)? Wie?

16.10.2007

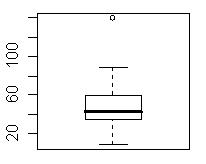
9. Betrachten Sie den Datensatz cpu.dat (vgl. Aufgabe 5)

(a) Berechnen Sie den

Mittelwert = sum(x)/length(x) = 48.23333,

den Median = 1/2(x[30/2]+x[30/2+1]) = 42,5

und den Modalwert (Modus) = die Klasse 28 bis 42 Sekunden. --> Mittelwert?

(b) Berechnen Sie die

Varianz = 703.1506

die Streuung =

und den Quartilabstand =

(c) Berechnen Sie die mittlere absolute Abweichung (MAD)

MAD = 20.0151

*(d) Ermitteln Sie die 5–Zahlen Zusammenfassung und zeichnen Sie einen Boxplot. Hinweis: Die R–Funktionen lauten fivenum() und boxplot().

> # ------------ Lageparameter
> #mittelwert
> sum(x)/n
[1] 48.23333
> 
> median(x)             #sort(x)[length(x)/2]
[1] 42.5
> 
> var(x)
[1] 703.1506
> 
> #Modus
> ModusCpu<-table(x)
> ModusCpu[ModusCpu==max(ModusCpu)]
x
35 36 56 82 
 2  2  2  2 
> 
> # ------------ Streuparameter
> 
> #Spannweite
> max(x)-min(x)
[1] 130
> 
> #Quartilabstand
> quantile(x,p=0.75)-quantile(x,p=0.25)
75% 
 24 
> 
> #Standardabweichung
> sd(x)
[1] 26.51699
> 
>  
> #mittlere absolute Abweichung
> mad(x)
[1] 20.0151
> 
> # ----------- fivenum and boxplot
> fivenum(x)
[1]   9.0  34.0  42.5  59.0 139.0
> boxplot(x)

10. Wiederholen Sie Aufgabe 9 für den Datensatz concurrent.dat (vgl. Aufgabe 7).

11. Zeigen Sie, daß ein allgemeiner Ausdruck für das p–Quantile auf Basis eines klassierten Datensatzes gegeben

ist wie folgt: Ist Ki = (ui, oi] diejenige Klasse, in die das p–Quantile hineinfällt, so gilt: xp = ui + p − i−1 Xj=1 hj! oi − ui hi

(hj = relative Klassenhäufigkeit der j–ten Klasse) Überprüfen Sie die Gültigkeit des Ausdrucks an der Berechnung des Medians bzw. des Quartilabstands in Aufgabe 9 oder 10.

12. Anzahl der täglichen (blockierten) Intrusion–Versuche im Verlauf von zwei Wochen

56 47 49 37 38 60 50 43 43 59 50 56 54 58

Nach einer Änderung der Einstellungen der Firewall lauteten die Zahlen in den folgenden 20 Tagen:

53 21 32 49 45 38 44 33 32 43 53 46 36 48 39 35 37 36 39 45

Vergleichen Sie die Daten vor und nach der Änderung:

*(a) Konstruieren Sie Stem-and-Leaf–Plots. Hinweis: Die R–Funktion lautet stem().

(b) Bestimmen Sie Lage– und Streuungsparameter.

*(c) Bestimmen Sie die 5-Zahlen–Zusammenfassungen.

*(d) Zeichnen Sie (parallele) Box-Plots.

(e) Kommentieren Sie die Ergebnisse.

*13. Wie in der VO angesprochen, versucht man in der schließenden Statistik (u.a.) den empirisch gegebenen Verteilungen (Histogrammen) theoretische Verteilungen (Dichten) anzupassen. Man versuche dies wahlweise für den Datensatz resistor.dat (Aufgabe 6) oder concurrent.dat (Aufgabe 7) mit der Anpassung

einer Normaldichte. Für die beiden Parameter dieser Verteilung (μ, �2) nehme man die entsprechenden empirischen Größen (x, s2).

14.

(a) Wieviele verschiedene Passwörter, bestehend aus 8 Zeichen, kann man aus einem Alphabet, bestehend aus 10 Ziffern, 26 Klein– und 26 Großbuchstaben, bilden?

m = (10+26+26)⁸ = 218 340 105 584 896

(b) Angenommen, ein Spy–Programm kann pro Sekunde 1 Million Passwörter verarbeiten. Wie lange braucht es für alle möglichen Passwörter? Wie lange braucht es im Durchschnitt, um Ihr persönliches Passwort zu finden?

das Spy Programm benötigt maximal time = m/1000000 = 218 340 105.584896 Sekunden.

das Spy Programm findet mein persönliches Passwort im Durchschnitt nach med(time) = (time+1)/2 = 109170053.292448 Sekunden.

(c) Mit welcher Wahrscheinlichkeit findet das Spy–Programm von (b) innerhalb einer Woche Ihr persönliches Passwort?

Die Wahrscheinlichkeit gibt an mit welcher Erwartung ein bestimmtes Ereignis eintreten wird. Der Wertebereich liegt zwischen 0 und 1 [0 - 1].

1 Woche hat 604800 Sekunden.

W=1 Woche/m = 604800/218,3*10⁶ = 2,77*10^-3

(d) Beantworten Sie die Fragen (a) bis (c), wenn Großbuchstaben bei der Bildung von Passwörtern nicht verwendet werden.

m = (10+26)⁸ = 2 821 109 907 456

max 2 821 109 Sekunden

Durchschnitt: 1 410 555,453728 Sekunden

W(1Woche) = 0,214

15. In einem Array der Länge n werden zufällig k (≤ n) Daten abgelegt

Also zunächst mal ein Beispiel: n=10

0 1 2 3 4 5 6 7 8 9 oder 2 - 2 - 3 - - 4 7 5

(a) Mit welcher Wahrscheinlichkeit kommt es dabei zu Mehrfachbelegungen?

(b) Wie groß muß k für n = 100 mindestens sein, damit diese Wahrscheinlichkeit größer als 0.5 (größer als 0.9) ist?

(c) Beantworten Sie (b) für n = 365. (Bem.: Diesen Fall nennt man auch „Geburtstagsproblem“.)

16. Eine Variante des „Geburtstagsproblems“ (vgl. Aufgabe 15(c))

Sie wollen jemanden finden, der am selben Tag wie Sie geboren ist. Welche Mindestanzahl von Personen müssen Sie befragen, damit die Wahrscheinlichkeit dafür etwa 1/2 beträgt? Wieviele, wenn die Wahrscheinlichkeit dafür mindestens 0.99 sein soll?