User:Zelenka/Statistics/exercises 25.05.2008

From eqqon

(Difference between revisions)

Zelenka (Talk | contribs)
(New page: ===3.=== ;Ist x1, . . . , xL eine Binärfolge der Länge L, so heißt die Teilfolge <math>x_{i+1}, . . . , x_{i+k}</math> ein Lauf (engl. run) der Länge k, falls: :(1) i = 0 oder <math>x_...)
Newer edit →

Revision as of 22:16, 24 May 2008

3.

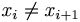
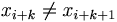
Ist x1, . . . , xL eine Binärfolge der Länge L, so heißt die Teilfolge $x i + 1,..., x i + k$ ein Lauf (engl. run) der Länge k, falls: (1) i = 0 oder $x_i \neq x_{i+1}$; (2) $x i + 1 = ... = x i + k$; (3) $i + k = L$ oder $x_{i+k} \neq x_{i+k+1}$

Ist beispielsweise L = 10 und lautet die Binärfolge:

0 0 1 0 0 0 1 1 0 0

so gibt es 5 Läufe mit den Längen 2, 1, 3, 2, 2.

Die Abfrage einer Tastatur ist manchmal fehlerhaft. Die Fehlerwahrscheinlichkeit ist Gleichförmig verteilt. Wie hoch ist die Wahrscheinlichkeit einer Fehlfunktion wenn man die Tastatur 2 mal abfragt und dabei das gleiche bitmuster aller 184 Tasten einlesen muss?

#Bestimmung der Zahl der Läufe für Binärfolge x
RunNumber <- function(x) {
n <- length(x)
z <- x
z[n+1] <- ifelse(x[n]==0, 1, 0)
y <- abs(diff(z))
Index1 <- c(1:n)
Index <- c(0,Index1[y==1])
Number <- length(diff(Index))
return(Number) }

#Simulation
N <- 500
L <- 60
x <- matrix(rbinom(N*L, 1, 1/2), nrow=N)
NumberRuns <- apply(x, 1, RunNumber)

#Häufigkeitstabelle
tab1 <- table(NumberRuns)
mr <- as.numeric(names(tab1))
n1 <- min(mr)
n2 <- max(mr)
nk <- numeric(n2-n1+1)
nk[mr-n1+1] <- tab1
names(nk) <- n1:n2
par(mfrow=c(2,1))

#Stabdiagramm
barplot(nk/N, axis.lty=1, space=1, xlab="Anzahl der Läufe",
main=paste("L = ", L, " Nsim = ", N), col="orange2")

#Summenkurve
plot(ecdf(NumberRuns), verticals=TRUE, do.points=FALSE,
xlab="Anzahl der Läufe", ylab="Kum. rel. Häufigk.",
main="Summenkurve")
par(mfrow=c(1,1))