User:Zelenka/Statistics/excercises 8.1.2008
From eqqon
< User:Zelenka | Statistics(Difference between revisions)
Zelenka (Talk | contribs)
(New page: ;4.12) Ein Zufallspunkt (X, Y ) in der Ebene wird nach einer bivariaten Normalverteilung mit μ<sub>x</sub> = &mu<sub>y</sub> = 0, σ<sub>x</sub> = 2, σ<sub>y</sub> = 3 und &r...)
(New page: ;4.12) Ein Zufallspunkt (X, Y ) in der Ebene wird nach einer bivariaten Normalverteilung mit μ<sub>x</sub> = &mu<sub>y</sub> = 0, σ<sub>x</sub> = 2, σ<sub>y</sub> = 3 und &r...)
Latest revision as of 16:19, 11 December 2007
- 4.12) Ein Zufallspunkt (X, Y ) in der Ebene wird nach einer bivariaten Normalverteilung mit μx = &muy = 0, σx = 2, σy = 3 und ρ = 0 gewählt. ;Bestimmen Sie
- (a) W{Y > X}, W{X < 0, Y > 0};
- (b) die Wahrscheinlichkeit, daß der Punkt im Quadrat mit den Eckpunkten (1, 1), (1,−1), (−1,−1), (−1, 1) liegt.
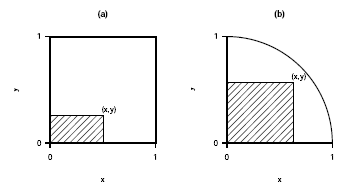
- 4.14) Ein Punkt (X, Y ) wird zufällig im (a) Einheitsquadrat; (b) Viertelkreis (Radius=1) gewählt. Bestimmen Sie den Erwartungswert des Umfangs des entstehenden Rechtecks.
- 4.15) Fortsetzung von Aufgabe 14
- Bestimmen Sie den Erwartungswert der Fläche des Rechtecks.
- 4.17) Fortsetzung von Aufgabe 3
- Bestimmen Sie den Korrelationskoeffizienten ρX,Y .
- 4.20) Die gemeinsame Dichte von (X, Y ) sei f(x, y) = C(x + y) für (x, y) 2 (0, 1) × (0, 1) und f(x, y) = 0 sonst.
- (a) Welchen Wert hat die Konstante C ?
- (b) Bestimmen Sie die beiden Randdichten von X und Y .
- (c) Bestimmen Sie den Korrelationskoeffizienten von X und Y .
- (d) Sind X und Y unkorreliert? unabhängig?
- 4.21) Fortsetzung von Aufgabe 20
- (a) Bestimmen Sie die bedingten Dichten von X|Y = y und von Y |X = x.
- (b) Bestimmen Sie die Regressionsfunktionen von X bezüglich Y und von Y bezüglich X.
- 4.26) Die logische Struktur eines Systems bestehend aus drei Komponenten sei gegeben wie folgt:
- Die Lebensdauern der Komponenten seien unabhängig und identisch verteilt mit Dichte f(x) = e−x I(0,1)(x). Bestimmen Sie die Verteilungsfunktion und die Dichte der Lebensdauer des Systems sowie den Mittelwert.