User:Zelenka/Statistics/exercises 30.10.2007
From eqqon
| Line 97: | Line 97: | ||
:W(<sup>n</sup>∪<sub>i=1</sub>A<sub>i</sub>) ≤ <sup>n</sup>∑<sub>Xi=1</sub> W(Ai) | :W(<sup>n</sup>∪<sub>i=1</sub>A<sub>i</sub>) ≤ <sup>n</sup>∑<sub>Xi=1</sub> W(Ai) | ||
</div> | </div> | ||
| + | |||
:(b) Zeigen Sie die Bonferroni’sche Ungleichung: | :(b) Zeigen Sie die Bonferroni’sche Ungleichung: | ||
<div style="font-size:130%;"> | <div style="font-size:130%;"> | ||
:W(<sup>n</sup>∩<sub>i=1</sub>A<sub>i</sub>) ≥ 1- <sup>n</sup>∑<sub>Xi=1</sub> W(Ai) | :W(<sup>n</sup>∩<sub>i=1</sub>A<sub>i</sub>) ≥ 1- <sup>n</sup>∑<sub>Xi=1</sub> W(Ai) | ||
</div> | </div> | ||
| + | |||
| + | Theorie: Bonferroni-Ungleichungen | ||
| + | Die Bonferroni-Ungleichungen sind Formeln, die zur Abschätzung der Wahrscheinlichkeit des Durchschnitts bzw. der Vereinigung von Ereignissen dienen. | ||
| + | Lösung: Zunächst beobachtet man, dass stets | ||
| + | :::n\i=1Ei =n[i=1Ei | ||
| + | :::gilt, und zwar nach der De Morgan’sche Regel: | ||
| + | :::(1\i=1Ai)c =1[i=1Aci , (1[i=1Ai)c =1\i=1Aci | ||
| + | |||
| + | |||
---- | ---- | ||
;5.) Ein neues Computervirus kann in ein System durch eine E-Mail oder durch das Internet eindringen. Es besteht eine Chance von 30%, daß man das Virus durch eine E-Mail, und eine 40% Chance, daß man es durch das Internet bekommt. Außerdem beträgt die Chance 15%, daß es simultan auf beiden Wegen eindringt. Wie groß ist unter diesen Vorgaben die Wahrscheinlichkeit, daß das Virus in das System gar nicht eindringt? | ;5.) Ein neues Computervirus kann in ein System durch eine E-Mail oder durch das Internet eindringen. Es besteht eine Chance von 30%, daß man das Virus durch eine E-Mail, und eine 40% Chance, daß man es durch das Internet bekommt. Außerdem beträgt die Chance 15%, daß es simultan auf beiden Wegen eindringt. Wie groß ist unter diesen Vorgaben die Wahrscheinlichkeit, daß das Virus in das System gar nicht eindringt? | ||
| Line 106: | Line 116: | ||
---- | ---- | ||
;6.) Formulieren und beweisen Sie das Additionsthorem für drei Ereignisse A, B, C. (Hinweis: Die Gültigkeit des Theorems für zwei Ereignisse darf vorausgesetzt werden.) | ;6.) Formulieren und beweisen Sie das Additionsthorem für drei Ereignisse A, B, C. (Hinweis: Die Gültigkeit des Theorems für zwei Ereignisse darf vorausgesetzt werden.) | ||
| + | <div style="white-space:pre;"> | ||
| + | W(AvBvC) = W(A) + W(B) +W(C) - W(AnB) - W(AnC) - W(BnC) + W(AnBnC) | ||
| + | |||
| + | Zuerst hab ich mir überlegt wie ich AvBvC noch darstellen kann. Dabei bin ich auf folgenden Ausdruck gekommen: | ||
| + | |||
| + | (A v B v C) = A v (-A n B) v (-A n -B n C) | ||
| + | |||
| + | Danach hab ich mir überlegt wie ich B und C noch darstellen kann. | ||
| + | |||
| + | B = (A n B) v (-A n B) | ||
| + | C = (A n C) v (B n C) v (-A n -B n C) / (A n B n C) | ||
| + | |||
| + | Danach hab ich die Wahrscheinlichkeiten angeschrieben und dann subtrahiert. | ||
| + | |||
| + | W(A v B v C) = W(A) + W(-A n B) + W(-A n -B n C) | ||
| + | W(B) = W(AnB) + W(-A n B) | ||
| + | W(C) = W(AnC) + W(BnC) + W(-A n -B n C) - W(An B n C) | ||
| + | |||
| + | |||
| + | W(A v B v C) = W(A) + W(-A n B) + W(-A n -B n C) | ||
| + | - W(B) = - W(AnB) - W(-A n B) | ||
| + | - W(C) = - W(AnC) - W(BnC) - W(-A n -B n C) + W(An B n C) | ||
| + | __________________________________________________ ______________ | ||
| + | W(AvBvC) - W(B) - W(C) = W(A) -W(AnB) - W(AnC) - W(BnC) + W(AnBnC) | ||
| + | |||
| + | So und jetzt noch W(B) und W(C) rübergeben und dann steht der Ausdruck von oben da. | ||
| + | |||
| + | W(AvBvC) = W(A) + W(B) + W(C) -W(AnB) - W(AnC) - W(BnC) + W(AnBnC) | ||
| + | |||
| + | </div> | ||
---- | ---- | ||
;7.) Die 8 Titel auf einer CD werden in zufälliger Reihenfolge abgespielt. Mit welcher Wahrscheinlichkeit wird dabei kein Titel an der auf der CD angegebenen Stelle wiedergegeben? (Hinweis: Verwenden Sie das Additionstheorem mit Ai = Der i–te Titel wird an i–ter Stelle wiedergegeben.) | ;7.) Die 8 Titel auf einer CD werden in zufälliger Reihenfolge abgespielt. Mit welcher Wahrscheinlichkeit wird dabei kein Titel an der auf der CD angegebenen Stelle wiedergegeben? (Hinweis: Verwenden Sie das Additionstheorem mit Ai = Der i–te Titel wird an i–ter Stelle wiedergegeben.) | ||
Latest revision as of 13:13, 30 October 2007
- 1.) A, B, C seien drei Ereignisse. Ermitteln Sie möglichst einfache Ausdrücke für die zusammengesetzten Ereignisse, daß von A, B, C
(a) nur A eintritt; W = A \ (B ∪ C) (f) keines eintritt; W = M \ ( A ∪ B ∪ C) (b) A und C, aber nicht B eintritt; W = (A ∩ C) \ B (g) höchstens eines eintritt; W = M \ (A ∩ B ∩ C) (c) zumindest eines eintritt; W = A ∪ B ∪ C (h) höchstens zwei eintreten; W = (A ∩ B) ∪ (A ∩ C) ∩ (B ∪ C) (d) zumindest zwei eintreten; W = (A ∩ B) ∪ (A ∩ C) ∪ (B ∩ C) (i) genau zwei eintreten; W = A ∩ B) ∪ (A ∩ C) ∪ (B ∩ C) \ (A ∩ B ∩ C) (e) alle drei eintreten; W = (A ∩ B ∩ C) (j) höchstens drei eintreten. W = M
- 2.) Eine Münze wird solange geworfen, bis zum ersten Mal „Kopf“ geworfen wird.
- (a) Bestimmen Sie einen passenden Wahrscheinlichkeitsraum (M, E,W) und zeigen Sie, daß W(M) = 1.
- Merkmalraum
- Die Elemente des Merkmalraums M sind (K = 'Kopf', Z = 'Zahl') . M = { K, ZK, ZZK, ZZZK, ... }
- W(K) = 1/2
- W(ZK) = 1/2 * 1/2 = 1/4
- W(ZZK) = 1/2 * 1/2 * 1/2 = 1/8
- W(ZnK) = (1/2)n+1
- Für einen Merkmalraum gilt: Σ W(Ai) = 1
- Die Elemente W(ZnK) stellen eine geometrische Reihe dar, für die bei q < 1 der Grenzwert der Summe gilt: a0 * (1/(1-q))
- W(M) = 1/2 + (1/2)2 + (1/2)3 + ... + (1/2)n
- W(M) = (1/2) * (1 + 1/2 + (1/2)2 + ... + (1/2)(n−1)) = (1/2) * (1/(1 − 1/2)) = 1/2 * 2/1 = 1
- Ereignisfeld
- theoretisch ist das Ereignisfeld unbegrenzt. In diskreten E = P(M)
Die W-Verteilung ordnet jedem dieser Elemente die folgenden Wahrscheinlichkeiten zu: 1/2, 1/4, 1/8, 1/16, ...
- (b) Ermitteln Sie die Wahrscheinlichkeit für das Ereignis, daß der erste Kopf bei einem ungeraden Wurf kommt.
- W = 1/2 + (1/2)3 + (1/2)5 + ... + (1/2)2n+1
- W(M) = (1/2) * (1/(1 − 1/4)) = 1/2 * 4/3 = 4/6 = 2/3
- (c) Ermitteln Sie allgemein die Wahrscheinlichkeit mit der man öfter als x Mal werfen muß, bis zum ersten Mal Kopf kommt.
- W(öfter als x) = 1 - (Σ W(xn))
- (d) Simulieren Sie das Experiment auf Basis von R.
# wirf eine münze bis kopf kommt
WirfKopf <- function() {
result<-sample(0:1,1)
n<-1
while (result != 1) {
n<-n+1;
result<-sample(0:1,1);
}
return(n) }
# n versuche
n <- 1:10000;
# vektor für die maximalen würfe bis Kopf kommt
# (Klasseneinteilung)
xmax <- 1:15;
x <- c();
# bilde einen vektor mit xmax elementen
# und setze alle werte auf 0
for (i in xmax) {
x <- c(x, 0);
}
for (i in n) {
# a = anzahl der würfe bis kopf kommt
a<-WirfKopf()
# erhöhe die Anzahl in x[AnzahlBisKopf] um 1
x[a] <- x[a] + 1;
}
# Ausgabe der abs. Häufigkeiten der Würfe bis Kopf
print(x)
# Berechne die rel Häufigkeiten für x[AnzahlBisKopf]
x <- x / length(n);
print(x)
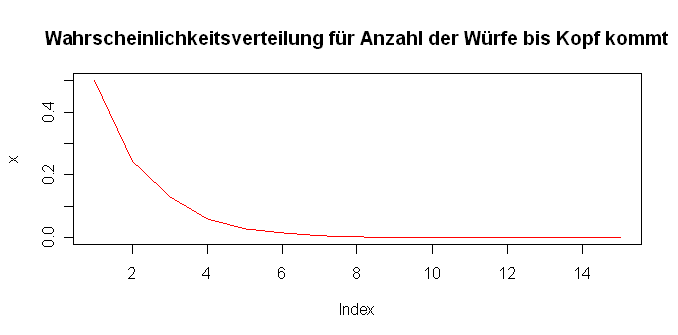
plot(x, type="l", col="red", main="Wahrscheinlichkeitsverteilung für Anzahl der Würfe bis Kopf kommt");
[1] 5016 2453 1305 615 297 155 81 32 23 12 6 2 2 1 0
[1] 0.5016 0.2453 0.1305 0.0615 0.0297 0.0155 0.0081 0.0032 0.0023 0.0012 0.0006 0.0002 [13] 0.0002 0.0001 0.0000
- 3.) Der Merkmalraum M bestehe aus allen Punkten, die in einem Quadrat mit den Eckpunkten (0, 0), (1, 0), (1, 1), (0, 1) liegen. Es sei W(A) = R RA dx dy.
- (a) Zeigen Sie, daß auf diese Weise eine W–Verteilung definiert wird. (*Wie lautet ein passendes Ereignisfeld?)
- (b) Bestimmen Sie W(A1) für A1 = {(x, y) : 0 < x < y < 1}.
- (c) Bestimmen Sie W(A2) für A2 = {(x, y) : 0 < x = y < 1}.
- (d) Bestimmen Sie W(A3) für A3 = {(x, y) : 0 < x/2 � y � 3x/2 < 1}.
- 4. Ai, i = 1, . . . , n, seien Ereignisse aus aus einem Ereignisfeld.
- (a) Zeigen Sie die Boole’sche Ungleichung:
- W(n∪i=1Ai) ≤ n∑Xi=1 W(Ai)
- (b) Zeigen Sie die Bonferroni’sche Ungleichung:
- W(n∩i=1Ai) ≥ 1- n∑Xi=1 W(Ai)
Theorie: Bonferroni-Ungleichungen Die Bonferroni-Ungleichungen sind Formeln, die zur Abschätzung der Wahrscheinlichkeit des Durchschnitts bzw. der Vereinigung von Ereignissen dienen. Lösung: Zunächst beobachtet man, dass stets
- n\i=1Ei =n[i=1Ei
- gilt, und zwar nach der De Morgan’sche Regel:
- (1\i=1Ai)c =1[i=1Aci , (1[i=1Ai)c =1\i=1Aci
- 5.) Ein neues Computervirus kann in ein System durch eine E-Mail oder durch das Internet eindringen. Es besteht eine Chance von 30%, daß man das Virus durch eine E-Mail, und eine 40% Chance, daß man es durch das Internet bekommt. Außerdem beträgt die Chance 15%, daß es simultan auf beiden Wegen eindringt. Wie groß ist unter diesen Vorgaben die Wahrscheinlichkeit, daß das Virus in das System gar nicht eindringt?
- 6.) Formulieren und beweisen Sie das Additionsthorem für drei Ereignisse A, B, C. (Hinweis
- Die Gültigkeit des Theorems für zwei Ereignisse darf vorausgesetzt werden.)
W(AvBvC) = W(A) + W(B) +W(C) - W(AnB) - W(AnC) - W(BnC) + W(AnBnC)
Zuerst hab ich mir überlegt wie ich AvBvC noch darstellen kann. Dabei bin ich auf folgenden Ausdruck gekommen:
(A v B v C) = A v (-A n B) v (-A n -B n C)
Danach hab ich mir überlegt wie ich B und C noch darstellen kann.
B = (A n B) v (-A n B) C = (A n C) v (B n C) v (-A n -B n C) / (A n B n C)
Danach hab ich die Wahrscheinlichkeiten angeschrieben und dann subtrahiert.
W(A v B v C) = W(A) + W(-A n B) + W(-A n -B n C) W(B) = W(AnB) + W(-A n B) W(C) = W(AnC) + W(BnC) + W(-A n -B n C) - W(An B n C)
W(A v B v C) = W(A) + W(-A n B) + W(-A n -B n C)
- W(B) = - W(AnB) - W(-A n B)
- W(C) = - W(AnC) - W(BnC) - W(-A n -B n C) + W(An B n C)
__________________________________________________ ______________
W(AvBvC) - W(B) - W(C) = W(A) -W(AnB) - W(AnC) - W(BnC) + W(AnBnC)
So und jetzt noch W(B) und W(C) rübergeben und dann steht der Ausdruck von oben da.
W(AvBvC) = W(A) + W(B) + W(C) -W(AnB) - W(AnC) - W(BnC) + W(AnBnC)
- 7.) Die 8 Titel auf einer CD werden in zufälliger Reihenfolge abgespielt. Mit welcher Wahrscheinlichkeit wird dabei kein Titel an der auf der CD angegebenen Stelle wiedergegeben? (Hinweis
- Verwenden Sie das Additionstheorem mit Ai = Der i–te Titel wird an i–ter Stelle wiedergegeben.)