User:Zelenka/Statistics/exercises 16.10.2007

From eqqon

< User:Zelenka | Statistics(Difference between revisions)
Jump to: navigation, search
(New page: ==16.10.2007== ;9. Betrachten Sie den Datensatz cpu.dat (vgl. Aufgabe 5) :(a) Berechnen Sie den ::Mittelwert = sum(x)/length(x) = 48.23333, ::den Median = 1/2(x[30/2]+x[30/2+1]) = 42,5 :...)
 
(2 intermediate revisions not shown)
Line 59: Line 59:
;10.  Wiederholen Sie Aufgabe 9 für den Datensatz concurrent.dat (vgl. Aufgabe 7).
;10.  Wiederholen Sie Aufgabe 9 für den Datensatz concurrent.dat (vgl. Aufgabe 7).
 +
 +
> # ------------ Lageparameter
 +
> #mittelwert
 +
> sum(x)/n
 +
[1] 17.954
 +
>
 +
> median(x)            #sort(x)[length(x)/2]
 +
[1] 17.55
 +
>
 +
> var(x)
 +
[1] 9.968249
 +
>
 +
> #Modus
 +
> ModusCpu<-table(x)
 +
> ModusCpu[ModusCpu==max(ModusCpu)]
 +
x
 +
14.8 15.8 16.2 17.1 17.2 21.7 23.9
 +
    2    2    2    2    2    2    2
 +
>
 +
> # ------------ Streuparameter
 +
>
 +
> #Spannweite
 +
> max(x)-min(x)
 +
[1] 12.2
 +
>
 +
> #Quartilabstand
 +
> quantile(x,p=0.75)-quantile(x,p=0.25)
 +
  75%
 +
4.05
 +
>
 +
> #Standardabweichung
 +
> sd(x)
 +
[1] 3.157253
 +
>
 +
>
 +
> #mittlere absolute Abweichung
 +
> mad(x)
 +
[1] 3.18759
 +
>
 +
> # ----------- fivenum and boxplot
 +
> fivenum(x)
 +
[1] 11.90 15.80 17.55 19.90 24.10
 +
> boxplot(x)
 +
>
 +
>
[[Image:Statistik ue 10.png]]
[[Image:Statistik ue 10.png]]
Line 107: Line 152:
::: W(1Woche) = 0,214
::: W(1Woche) = 0,214
 +
<div style="background-color:#ccffcc">
 +
;;;VORGETRAGEN
;15. In einem Array der Länge n werden zufällig k (≤ n) Daten abgelegt:
;15. In einem Array der Länge n werden zufällig k (≤ n) Daten abgelegt:
::: Also zunächst mal ein Beispiel: n=10
::: Also zunächst mal ein Beispiel: n=10
::: 0 1 2 3 4 5 6 7 8 9  oder  2 2 3 - - 4 7 5
::: 0 1 2 3 4 5 6 7 8 9  oder  2 2 3 - - 4 7 5
:(a) Mit welcher Wahrscheinlichkeit kommt es dabei zu Mehrfachbelegungen?
:(a) Mit welcher Wahrscheinlichkeit kommt es dabei zu Mehrfachbelegungen?
 +
 +
Die Wahrschinlichkeit f&uuml;r den ersten Platz im Array keine Mehrfachbelegung zu erhalten ist k g&uuml;nstige Werte von m m&ouml;glichen, also p(1) = m / m
 +
 +
Die Wahrschinlichkeit f&uuml;r den zweinten Platz im Array keine Mehrfachbelegung zu erhalten ist k-1 g&uuml;nstige Werte von m m&ouml;glichen, also p(1) = (m-1) / m
 +
 +
Allgemein: p(n) = (m-k+1) / m
 +
 +
Die Wahrscheinlichkeiten der Arrayplätze werden multipliziert um die Gesamtwahrscheinlichkeit zu erhalten: Q = &Pi; p(n)
 +
 +
Die Gegenwahrscheinlichkeit ist daher die gewünschte Wahrscheinlichkeit einer Mehrfachbelegung: P = 1 - Q = 1 - &Pi; p(n) = 1 - &Pi; ((m-k+1) / m)
 +
 +
Nach algebraischer Umformung erhält man:
::: p(n,k) = 1-( n! / ((n-k)! * n<sup>k</sup>)
::: p(n,k) = 1-( n! / ((n-k)! * n<sup>k</sup>)
 +
 +
> n<-100
 +
> k<-1:n
 +
>
 +
> p<-1-(factorial(n)/((factorial(n-k)*n^k)))
 +
>
 +
> plot(p)
 +
>
 +
> p
 +
  [1] 1.898481e-14 1.000000e-02 2.980000e-02 5.890600e-02 9.654976e-02 1.417223e-01 1.932189e-01
 +
  [8] 2.496936e-01 3.097181e-01 3.718435e-01 4.346591e-01 4.968466e-01 5.572250e-01 6.147858e-01
 +
  [15] 6.687158e-01 7.184084e-01 7.634631e-01 8.036743e-01 8.390130e-01 8.696005e-01 8.956804e-01
 +
  [22] 9.175875e-01 9.357183e-01 9.505031e-01 9.623823e-01 9.717867e-01 9.791222e-01 9.847592e-01
 +
  [29] 9.890266e-01 9.922089e-01 9.945462e-01 9.962369e-01 9.974411e-01 9.982855e-01 9.988685e-01
 +
  [36] 9.992645e-01 9.995293e-01 9.997034e-01 9.998161e-01 9.998878e-01 9.999327e-01 9.999603e-01
 +
  [43] 9.999770e-01 9.999869e-01 9.999926e-01 9.999960e-01 9.999978e-01 9.999988e-01 9.999994e-01
 +
  [50] 9.999997e-01 9.999998e-01 9.999999e-01 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 +
  [57] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 +
  [64] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 +
  [71] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 +
  [78] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 +
  [85] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 +
  [92] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 +
  [99] 1.000000e+00 1.000000e+00
 +
 +
[[Image:Statistik ue 15a.png]]
 +
:(b) Wie groß muß k für n = 100 mindestens sein, damit diese Wahrscheinlichkeit größer als 0.5 (größer als 0.9) ist?
:(b) Wie groß muß k für n = 100 mindestens sein, damit diese Wahrscheinlichkeit größer als 0.5 (größer als 0.9) ist?
-
:::  
+
::: k=13 | p >= 0,5
 +
::: k=22 | p >= 0,9
 +
 
:(c) Beantworten Sie (b) für n = 365. (Bem.: Diesen Fall nennt man auch „Geburtstagsproblem“.)
:(c) Beantworten Sie (b) für n = 365. (Bem.: Diesen Fall nennt man auch „Geburtstagsproblem“.)
 +
</div>
 +
 +
<div style="background-color:#ccffcc">
 +
;;;VORGETRAGEN
 +
;16. Eine Variante des „Geburtstagsproblems“ (vgl. Aufgabe 15(c)){{dp}} Sie wollen jemanden finden, der am selben Tag wie Sie geboren ist. Welche Mindestanzahl von Personen müssen Sie befragen, damit die Wahrscheinlichkeit dafür etwa 1/2 beträgt? Wieviele, wenn die Wahrscheinlichkeit dafür mindestens 0.99 sein soll?
 +
 +
Die Wahrscheinlichkeit an einem bestimmtem Tag Geburtstag zu haben ist p(1)= 1/365.
 +
 +
Die Wahrscheinlichkeit am einem bestimmtem Tag nicht Geburtstag zu haben ist daher q(1)=1-p
 +
 +
Bei 2 unabhängigen Versuchen gilt  q*q = q<sup>2</sup>
 +
 +
Die Wahrscheinlichkeit dass 2 Personen nicht gemeinsam Geburtstag haben ist daher q<sup>2</sup>
 +
 +
Wiederum die Gegenwahrschinlichkeit ist dann die Wahrscheinlichkeit, dass 2 Personen an einem Tag Geburtstag haben p = 1 - q<sup>2</sup> = 1 - (1 - p)<sup>2</sup> = 1 - (1 - (1 / 365))<sup>2</sup>
 +
 +
;Allgemein formuliert:
 +
 +
p(n) = 1 - (1 - 1 / m)<sup>n</sup>
 +
 +
Diesen Ausdruck kann man nun algebraisch umformulieren sodass man "n" erhält:
 +
 +
1 - p(n) = (1 - 1 / m)<sup>n</sup>
 +
 +
n = ln (1 - p(n)) / ln (1 - 1 / m)
 +
 +
;Ergebnisse
 +
:f&uuml;r p = 0,5{{dp}} 253 Personen
 +
:f&uuml;r p = 0,99{{dp}} 1679 Personen
-
;16. Eine Variante des „Geburtstagsproblems“ (vgl. Aufgabe 15(c)): Sie wollen jemanden finden, der am selben Tag wie Sie geboren ist. Welche Mindestanzahl von Personen müssen Sie befragen, damit die Wahrscheinlichkeit dafür etwa 1/2 beträgt? Wieviele, wenn die Wahrscheinlichkeit dafür mindestens 0.99 sein soll?
+
</div>

Latest revision as of 19:07, 16 October 2007

16.10.2007

9. Betrachten Sie den Datensatz cpu.dat (vgl. Aufgabe 5)
(a) Berechnen Sie den
Mittelwert = sum(x)/length(x) = 48.23333,
den Median = 1/2(x[30/2]+x[30/2+1]) = 42,5
und den Modalwert (Modus) = die Klasse 28 bis 42 Sekunden. --> Mittelwert?
(b) Berechnen Sie die
Varianz = 703.1506
die Streuung =
und den Quartilabstand =
(c) Berechnen Sie die mittlere absolute Abweichung (MAD)
MAD = 20.0151
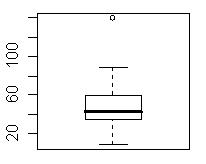
*(d) Ermitteln Sie die 5–Zahlen Zusammenfassung und zeichnen Sie einen Boxplot. Hinweis: Die R–Funktionen lauten fivenum() und boxplot(). 
> # ------------ Lageparameter
> #mittelwert
> sum(x)/n
[1] 48.23333
> 
> median(x)             #sort(x)[length(x)/2]
[1] 42.5
> 
> var(x)
[1] 703.1506
> 
> #Modus
> ModusCpu<-table(x)
> ModusCpu[ModusCpu==max(ModusCpu)]
x
35 36 56 82 
 2  2  2  2 
> 
> # ------------ Streuparameter
> 
> #Spannweite
> max(x)-min(x)
[1] 130
> 
> #Quartilabstand
> quantile(x,p=0.75)-quantile(x,p=0.25)
75% 
 24 
> 
> #Standardabweichung
> sd(x)
[1] 26.51699
> 
>  
> #mittlere absolute Abweichung
> mad(x)
[1] 20.0151
> 
> # ----------- fivenum and boxplot
> fivenum(x)
[1]   9.0  34.0  42.5  59.0 139.0
> boxplot(x)

Statistik ue 9.png

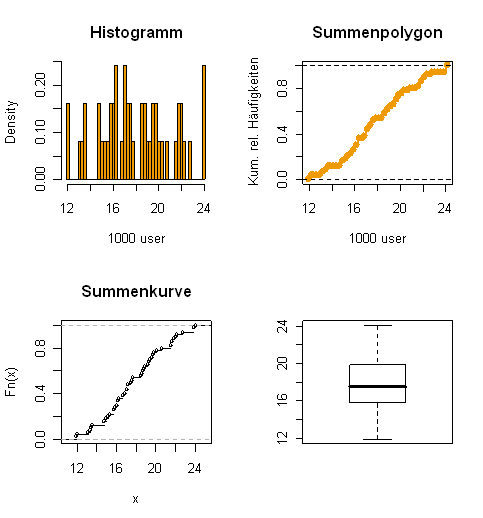
10. Wiederholen Sie Aufgabe 9 für den Datensatz concurrent.dat (vgl. Aufgabe 7). 
> # ------------ Lageparameter
> #mittelwert
> sum(x)/n
[1] 17.954
> 
> median(x)             #sort(x)[length(x)/2]
[1] 17.55
> 
> var(x)
[1] 9.968249
> 
> #Modus
> ModusCpu<-table(x)
> ModusCpu[ModusCpu==max(ModusCpu)]
x
14.8 15.8 16.2 17.1 17.2 21.7 23.9 
   2    2    2    2    2    2    2 
> 
> # ------------ Streuparameter
> 
> #Spannweite
> max(x)-min(x)
[1] 12.2
> 
> #Quartilabstand
> quantile(x,p=0.75)-quantile(x,p=0.25)
 75% 
4.05 
> 
> #Standardabweichung
> sd(x)
[1] 3.157253
> 
> 
> #mittlere absolute Abweichung
> mad(x)
[1] 3.18759
> 
> # ----------- fivenum and boxplot
> fivenum(x)
[1] 11.90 15.80 17.55 19.90 24.10
> boxplot(x)
> 
>

Statistik ue 10.png

11. Zeigen Sie, daß ein allgemeiner Ausdruck für das p–Quantile auf Basis eines klassierten Datensatzes gegeben

ist wie folgt: Ist Ki = (ui, oi] diejenige Klasse, in die das p–Quantile hineinfällt, so gilt: xp = ui + p − i−1 Xj=1 hj! oi − ui hi

(hj = relative Klassenhäufigkeit der j–ten Klasse) Überprüfen Sie die Gültigkeit des Ausdrucks an der Berechnung des Medians bzw. des Quartilabstands in Aufgabe 9 oder 10.

12. Anzahl der täglichen (blockierten) Intrusion–Versuche im Verlauf von zwei Wochen
56 47 49 37 38 60 50 43 43 59 50 56 54 58

Nach einer Änderung der Einstellungen der Firewall lauteten die Zahlen in den folgenden 20 Tagen:

53 21 32 49 45 38 44 33 32 43 53 46 36 48 39 35 37 36 39 45

Vergleichen Sie die Daten vor und nach der Änderung:

*(a) Konstruieren Sie Stem-and-Leaf–Plots. Hinweis: Die R–Funktion lautet stem().
(b) Bestimmen Sie Lage– und Streuungsparameter.
*(c) Bestimmen Sie die 5-Zahlen–Zusammenfassungen.
*(d) Zeichnen Sie (parallele) Box-Plots.
(e) Kommentieren Sie die Ergebnisse.
*13. Wie in der VO angesprochen, versucht man in der schließenden Statistik (u.a.) den empirisch gegebenen Verteilungen (Histogrammen) theoretische Verteilungen (Dichten) anzupassen. Man versuche dies wahlweise für den Datensatz resistor.dat (Aufgabe 6) oder concurrent.dat (Aufgabe 7) mit der Anpassung

einer Normaldichte. Für die beiden Parameter dieser Verteilung (μ, �2) nehme man die entsprechenden empirischen Größen (x, s2).

14.
(a) Wieviele verschiedene Passwörter, bestehend aus 8 Zeichen, kann man aus einem Alphabet, bestehend aus 10 Ziffern, 26 Klein– und 26 Großbuchstaben, bilden?
m = (10+26+26)8 = 218 340 105 584 896
(b) Angenommen, ein Spy–Programm kann pro Sekunde 1 Million Passwörter verarbeiten. Wie lange braucht es für alle möglichen Passwörter? Wie lange braucht es im Durchschnitt, um Ihr persönliches Passwort zu finden?
das Spy Programm benötigt maximal time = m/1000000 = 218 340 105.584896 Sekunden.
das Spy Programm findet mein persönliches Passwort im Durchschnitt nach med(time) = (time+1)/2 = 109170053.292448 Sekunden.
(c) Mit welcher Wahrscheinlichkeit findet das Spy–Programm von (b) innerhalb einer Woche Ihr persönliches Passwort?
Die Wahrscheinlichkeit gibt an mit welcher Erwartung ein bestimmtes Ereignis eintreten wird. Der Wertebereich liegt zwischen 0 und 1 [0 - 1].
1 Woche hat 604800 Sekunden.
W=1 Woche/m = 604800/218,3*106 = 2,77*10-3
(d) Beantworten Sie die Fragen (a) bis (c), wenn Großbuchstaben bei der Bildung von Passwörtern nicht verwendet werden.
m = (10+26)8 = 2 821 109 907 456
max 2 821 109 Sekunden
Durchschnitt: 1 410 555,453728 Sekunden
W(1Woche) = 0,214
VORGETRAGEN
15. In einem Array der Länge n werden zufällig k (≤ n) Daten abgelegt
Also zunächst mal ein Beispiel: n=10
0 1 2 3 4 5 6 7 8 9 oder 2 2 3 - - 4 7 5
(a) Mit welcher Wahrscheinlichkeit kommt es dabei zu Mehrfachbelegungen?

Die Wahrschinlichkeit für den ersten Platz im Array keine Mehrfachbelegung zu erhalten ist k günstige Werte von m möglichen, also p(1) = m / m

Die Wahrschinlichkeit für den zweinten Platz im Array keine Mehrfachbelegung zu erhalten ist k-1 günstige Werte von m möglichen, also p(1) = (m-1) / m

Allgemein: p(n) = (m-k+1) / m

Die Wahrscheinlichkeiten der Arrayplätze werden multipliziert um die Gesamtwahrscheinlichkeit zu erhalten: Q = Π p(n)

Die Gegenwahrscheinlichkeit ist daher die gewünschte Wahrscheinlichkeit einer Mehrfachbelegung: P = 1 - Q = 1 - Π p(n) = 1 - Π ((m-k+1) / m)

Nach algebraischer Umformung erhält man:

p(n,k) = 1-( n! / ((n-k)! * nk) 
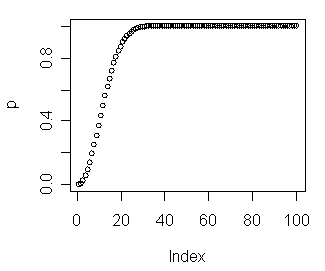
> n<-100
> k<-1:n
> 
> p<-1-(factorial(n)/((factorial(n-k)*n^k)))
> 
> plot(p)
> 
> p
  [1] 1.898481e-14 1.000000e-02 2.980000e-02 5.890600e-02 9.654976e-02 1.417223e-01 1.932189e-01
  [8] 2.496936e-01 3.097181e-01 3.718435e-01 4.346591e-01 4.968466e-01 5.572250e-01 6.147858e-01
 [15] 6.687158e-01 7.184084e-01 7.634631e-01 8.036743e-01 8.390130e-01 8.696005e-01 8.956804e-01
 [22] 9.175875e-01 9.357183e-01 9.505031e-01 9.623823e-01 9.717867e-01 9.791222e-01 9.847592e-01
 [29] 9.890266e-01 9.922089e-01 9.945462e-01 9.962369e-01 9.974411e-01 9.982855e-01 9.988685e-01
 [36] 9.992645e-01 9.995293e-01 9.997034e-01 9.998161e-01 9.998878e-01 9.999327e-01 9.999603e-01
 [43] 9.999770e-01 9.999869e-01 9.999926e-01 9.999960e-01 9.999978e-01 9.999988e-01 9.999994e-01
 [50] 9.999997e-01 9.999998e-01 9.999999e-01 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 [57] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 [64] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 [71] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 [78] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 [85] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 [92] 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
 [99] 1.000000e+00 1.000000e+00

Statistik ue 15a.png

(b) Wie groß muß k für n = 100 mindestens sein, damit diese Wahrscheinlichkeit größer als 0.5 (größer als 0.9) ist?
k=13 | p >= 0,5
k=22 | p >= 0,9
(c) Beantworten Sie (b) für n = 365. (Bem.: Diesen Fall nennt man auch „Geburtstagsproblem“.)
VORGETRAGEN
16. Eine Variante des „Geburtstagsproblems“ (vgl. Aufgabe 15(c)): Sie wollen jemanden finden, der am selben Tag wie Sie geboren ist. Welche Mindestanzahl von Personen müssen Sie befragen, damit die Wahrscheinlichkeit dafür etwa 1/2 beträgt? Wieviele, wenn die Wahrscheinlichkeit dafür mindestens 0.99 sein soll?

Die Wahrscheinlichkeit an einem bestimmtem Tag Geburtstag zu haben ist p(1)= 1/365.

Die Wahrscheinlichkeit am einem bestimmtem Tag nicht Geburtstag zu haben ist daher q(1)=1-p

Bei 2 unabhängigen Versuchen gilt q*q = q2

Die Wahrscheinlichkeit dass 2 Personen nicht gemeinsam Geburtstag haben ist daher q2

Wiederum die Gegenwahrschinlichkeit ist dann die Wahrscheinlichkeit, dass 2 Personen an einem Tag Geburtstag haben p = 1 - q2 = 1 - (1 - p)2 = 1 - (1 - (1 / 365))2

Allgemein formuliert

p(n) = 1 - (1 - 1 / m)n

Diesen Ausdruck kann man nun algebraisch umformulieren sodass man "n" erhält:

1 - p(n) = (1 - 1 / m)n

n = ln (1 - p(n)) / ln (1 - 1 / m)

Ergebnisse
für p = 0,5: 253 Personen
für p = 0,99: 1679 Personen
Retrieved from "http://eqqon.com/index.php/User:Zelenka/Statistics/exercises_16.10.2007"